Flat Earth Follies: The Horizon Always Rises To Eye Level
Flat Earth Claim
The Horizon Always Rises To Eye Level
The Facts
What I want to know is, how exactly did you measure that?
It certainly does not look "eye-level" to me.
In fact, trivial observation shows that it drops by pretty much EXACTLY the amount we would expect on an Earth with a radius of approximately 3959 miles.
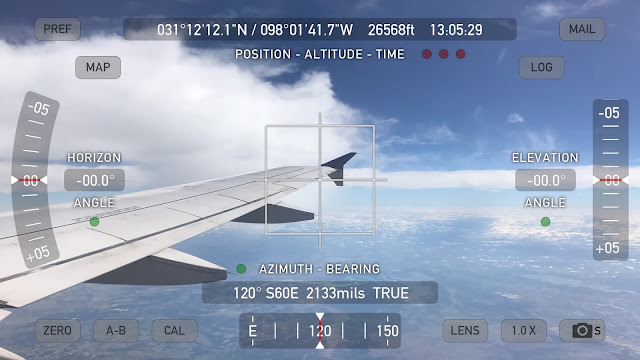
I have a Theodolite application on my iPhone 7 Plus which uses the accelerometers to position a reticle in the camera view marking out level & plumb and has indicators showing the angle of the camera in relationship to level. In the image below I have purposefully tilted the camera along two axes so you can see that the reticle has turned red indicating that my view is very tilted but it has aligned itself to the horizon while the white cross-marks simply mark center of the camera view.
So it doesn't matter if my phone or the plane or anything else is tilted, the angles indicated by the Horizon Angle and Elevation Angle indicators are relative to LEVEL.
 |
| Figure 1 |
And yes, these are from a different flight so I'm on opposite sides of different planes, at different times. I didn't think to take the above picture until my return flight but I wanted to show readers that the reticle finds LEVEL with our view regardless of what the camera is doing.
If the Earth is approximately a sphere with radius R = 3959 miles or 20903520 feet we would expect that a viewer at greater and greater heights would (using the left-side example here):
 |
| Figure 2 |
#1 see an increasingly distant horizon equal to equation (1) above where distance to the horizon (d):
- d = √h √(h+2R)
#2 that the angle down to the horizon would thus be equal to:
- horizon dip angle = arcsin(d/(R+h))
Armed with this information we can now look at two examples I captured.
Example #1
h=24854 feet
R=20903520 (Earth radius in feet)
d=1019651.849' (about 193 miles to the horizon) [wolfram|alpha]
horizon dip angle = ~2.79° [wolfram|alpha]
 |
| Figure 3 - Example 1 |
There are a few sources of error here such as clouds, particulates in the atmosphere, and refraction affecting our true horizon so we cannot make an exact measurement. Let's see if this holds...
Example #2
Now we're up much higher...
h=38805 feet
R=20903520 (Earth radius in feet)
d=1274295.105' (about 241 miles to the horizon) [wolfram|alpha]
horizon dip angle = ~3.49° [wolfram|alpha]
 |
| Figure 4 - Example 2 |
 |
| Figure 5 |
This is, IN NO WAY, "rising to eye level" - this is the exact opposite of that.
In fact, let's watch a movie showing this horizon drop in action aboard a drone:
Here is a video from the cockpit of a commercial flight showing the Horizon angle:
Here is another video on this subject:
Conclusion
Flat Earth is flat out busted - there is no excuse for such shoddy work. Anyone claiming this is either knowingly a liar or lying in the sense that they haven't actually tested it but are making the assertion AS IF they know what they are talking about, when they very clearly do not.
They are already back-peddling and making excuses.
@ColdDimSum @judekatttt @600jefe @wordofsock @grunzwanzling42 @Fuelie327 Eye level isn't correct term. A ball would get lower as u climb up.— NASA Lies (@Portland_Ghosts) October 22, 2016
Funny that you have to make excuses as to why YOUR claims fail and end up looking exactly like an oblate spheroid Earth and, as I showed, the horizon getting lower as you climb up is exactly what we observe and it lowers an amount GREATER than a flat plane would because the curvature drops off at an exponential rate the higher we get.
The angle would be trivial to calculate on a flat plane Earth because RISE/RUN would give you the slope and the inverse tangent of a slope is an angle. But Flat Earth can't even tell you why your distance increases with altitude (except by their false appeal to perspective) or by how much.
But let's try that with our second example:
rise = h = 38805'
run = d = 1274295.105'
Gives us an angle of 1.744° [wolfram|alpha] from tan⁻¹(38805/1274295.105)
So toss this on the pile of Flat Earth Failures.
2017-09-14 Follow Up on Mike F
Our friend Make F writes:
>> Lots of million dollar words and mathematical equations, is that supposed to blow us away? Are we supposed to say "wow this guy is smart he must really have this all figured out"? 1st of all, any photographer will tell you that if your camera is level, the horizon will be exactly in the middle of your shot regardless of where the shot is taken.
Funny, because I took those shots too -- now, looking at these shots, can you tell me what the angle between LEVEL and the horizon is? You can't because it isn't being measured so we would have to GUESS AT IT.
Mike F also writes:
>>> Why did you tilt your camera?
SO I COULD MEASURE THE ANGLE BETWEEN LEVEL AND WHERE THE HORIZON IS.
Do you understand now?
These images also show that NOTHING else changes except the ANGLE indicator allows us to MEASURE the angle between level and where the horizon actually is (not at eye-level).
>>> All you need to do to confirm that the horizon always rises to eye level is put your camera on a perfectly level surface and snap a picture at various heights
The Theodolite function tells us when the camera is level as I demonstrated in the first first image on this page -- REGARDLESS of the tilt or orientation of the camera the colored reticle MARKS LEVEL from our position and the Horizon & Elevation angle indicators show you how tilted you are from level in each plane.
>> Every single shot will feature the horizon in the exact middle because... the horizon always rises to eye level. What a complete waste of time your test and accompanying novel was!! Go do it again with a level angle next time genius!
That is a complete lie and I have demonstrated this repeatedly.
More importantly I've shown YOU how to do the test yourself... where are YOUR images?
While I'm here -- let's do this with a water level:
Or watch Sly's other excellent video on the subject:
Now, the REAL question here is, will you
A) Admit your error full stop?
B) Pivot and throw out some other UTTER BULLSHIT lies?
C) Crawl back under your rock?
My history with Flat Earthers suggests B. But maybe you'll surprise me.
















Comments
Post a Comment