clair002

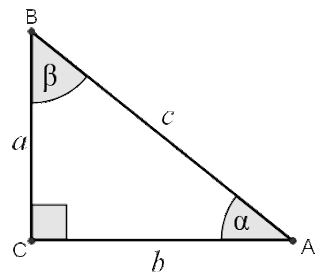
Can we know the shape of the Earth? or How Al-Biruni Calculated the Circumference of the Earth Using a Mountain in the 11th century As you might recall from my earlier posts, I've used the Sun at local Solar Noon (when the Sun is at its zenith) on the Equinox as a way to know the shape of the Earth.  But all we need is some point that is high enough to be seen at some significant distance and Mountain peaks are much easier to experiment with than a moving Sun. If the ground is a flat plane then we can simply triangulate using the mountain peak at different distances and get the SAME answer for the height using simple trigonometry: Figure 1 For example, if the ground was flat , we could find h by simply measuring our angle  α at two different distances, where  Δ d is the distance between the two observation points using the formula:     Δd  * tan(α₀) * tan(α₁) h = ----------------------       tan(α₁) - tan(α₀) Can you prove that? This ...

Flat Earth Claim The Earth is Flat! 100% Video Proof. Globe Earth Debunked GoFast July 14, 2014 Rocket Launch Proves the Earth is Flat because you can see the moon. Figure 1. The Claim Also here  and Reffi made a video about it. Analysis Prediction - this will consist of more (hopefully well-intentioned) Flat Earth misrepresentations, misunderstandings, and conclusion jumping, as evidenced in the title of Reffi's video: The Earth is Flat! 100% Video Proof. Globe Earth Debunked This implies they have the necessary skills and have taken the necessary care in evaluating the evidence and I think it becomes evident that they do not have the necessary skills and have not taken the necessary care in evaluating the evidence here.  I hope I have done a better job, but it is foolish to call ANY analysis "100% Proof" of anything.  So I simply offer my refutation with as much detail as I can. The Scene Somewhere in the Black Rock Desert, Nevada Morning July 14, 2014 14:32 UTC / 07:3...

Flat Earth Claim We couldn't get past the Van Allen Belts because it would be too much radiation. Analysis Why would I do an Analysis when this awesome page already exists? Apollo and the Van Allen Belts  an estimate of the radiation dose received Robert A. Braeunig His conclusion? Based on my analysis of electrons, protons, and bremsstrahlung, the predicted total dose received by the Apollo 11 astronauts as a consequence of their transits of the Van Allen radiation belts was only about 32 mrem, or 0.016 rads (all from protons ≥100 MeV). This shows that the Apollo trajectories though the VARB were not only survivable, but that the radiation doses received were inconsequential. Of course the VARB were not the only source of radiation to which the crews were exposed. To record the actual skin doses, the astronauts worn dosimeters. These dosimeter measurements for all the Apollo missions are summarized in Table 8 (Apollo 7 and 9 were Earth orbit missions).

Here is a picture of the majestic Mt. Rainier which rises 14,410 feet above the nearby Pacific ocean, taken from Lake Washington, about 55 miles / 88513.9 meters away (circa 47.604669°N 122.235966°W) Associated Press, 2006 The next image is also of Mt. Rainier but taken from about 130 miles / 209215 meters away over the Strait of Juan de Fuca by djboptics from Cadboro Bay (circa 48.454580°N 123.286889°W). Mt. Rainier, by @djboptics By scaling the images and matching them up as best we can (the Cadboro Bay image is about 9° further counter-clockwise around Rainier than the Lake Washington image) we can see that a substantial fraction of the mountain is missing! Is the alignment exactly perfect? No -- but the major features are well aligned vertically and horizontally. And this matches the scale expected from the angular size calculations below. Mount Rainier viewed from 55 miles vs 130 miles - scaled overlay It is very plain to see the effect of Earth curvature here on the apparent h...

Flat Earth Claim: The ISS is going too fast to take unblurred pictures! The Facts: This is what comes from people being mathematically illiterate. The orbital velocity of the ISS is about 17,150 miles per hour or about 4.76 miles per second.  That sure SEEMS fast, golly gee.  But if that is where you stopped in your thought process then you will come to false conclusions because you have ignored critical variables in the question. The main variables in photographic exposures are lighting, distance, film speed, shutter speed, and aperture. From this article in PetaPixel we find that they commonly use the 'Sunny 16' rule which says: On a sunny day set aperture to f/16 and shutter speed to the reciprocal of the ISO film speed/setting for a subject in direct sunlight. So at f/16, ISO 200 the resulting shutter speed is stated as "often 1/200". So we take our 4.76 miles per second and divide it by 200 which means the ISS moves approximately 0.0238th of a mile over th...

Flat Earth Claim Planes would have to constantly pitch down to fly! Short Version In the Globe model "LEVEL" follows a sphere of uniform gravity potential. Feel free to disprove that is the case if you can but that is the model. In an airplane, Elevator Trim simply controls the RATE of pitch of an aircraft - not the actual pitch of the plane. A 747 flying at 35,000' would have a flight circumference of  about 2π*(3959+(35000/5280)) ≈ 24916 miles Flying at 570 miles per hour, this plane would fly a fraction of the 360° around given by 360*570/24916 Since that's 1 hour we can divide by 60 to get the degrees per hour: 360*570/24916/60 ≈ 0.137°/minute That is down in the noise since pitch rate is affected by temperature, density, power, and control settings on the plane you simply trim the plane for as close to ZERO vertical speed as you can and you've automatically compensated for all of them at once.  Of course, on a 747 computers do that.  In a small plane the pitc...